1-13: Impact of Clouds on the Radiation Balance

RealAudio version of the learning unit

In previous lectures we have discussed the concept of infrared, or longwave, radiation and its importance to the global energy balance. To this point, however, we have not given a quantitative description of this concept. In this lecture we will discuss the mathematical form of this concept and demonstrate how it is useful in understanding measurements taken from satellites.

The amount of energy radiated from a body (such as the earth or a cloud) per unit area per unit time is given by the Stefan-Boltzmann equation given in the accompanying image. The emissivity is a property of the radiating object, but its value is usually near 1. The Stefan-Boltzmann constant has a value of 5.6696 x 10-8 Wm-2deg-4. The effective radiating temperature must be expressed using the Kelvin temperature scale (0 K being absolute zero and 273 $K\; =\; 0oC$) for this formula to make any sense. The fact that the temperature is raised to the fourth power means that even a small change in temperature translates into a large change in radiated energy.

Earth Radiation (Infrared Radiation)

Recall from the lecture on atmospheric structure and circulation that the temperature of the atmosphere decreases with height. Clouds will have temperatures approximately equivalent to the surrounding air, so high clouds will be expected to have lower temperatures than low clouds. From what we have just discussed, therefore, we would expect high clouds to emit much less infrared radiation than low clouds, and low clouds will likely emit less infrared radiation than the underlying surface of the earth. Therefore, even though all clouds are somewhat uniform in reflecting solar (visible) radiation from their top sides, they differ significantly in the amount of energy they emit upward by infrared radiation.

Our discussion from the last lecture included the topic of reflection of solar radiation from particles (dust, soot, volcanic materials, etc.) in the atmosphere. It was noted that volcanoes can cause temporary global cooling due to this effect. The next image (currently unavailable) shows the cooling caused by three recent volcanoes: Agung in the 1960s, El Chichon in Mexico in the mid 1980s, and Mt. Pinatubo in the Philippines in 1991. In each case, the temperature dropped immediately and gradually recovered over a period of about three years. Global climate models have been used to estimate the effects of such volcanoes from known volumes of particulate material put into the atmosphere. These calculations have been quite accurate in estimating the effects on global climate.

The accompanying photograph, produced by the Earth Radiation Budget Experiment (ERBE) program of the National Oceanic and Atmospheric Administration (NOAA) (Harrison et al, 1988), shows a map of outgoing longwave radiation, in Wm-2, for the month of April 1985 under clear-sky conditions. Regions colored in red and purple define regions of high amount of infrared radiation leaving the earth, and green and blue colors denote low IR values. From the Stefan-Boltzmann equation, we can also say that the radiating regions colored red and purple are warmer than those colored green and blue. As expected, the tropical and subtropical regions have the highest outgoing radiation (and temperature) and polar regions have lowest values. Very careful inspection, however, will reveal that some areas in the equatorial regions over land have substantially lower temperatures than adjacent subtropical areas to the north or south. Can you explain this?

Earth Radiation Budget Experiment (ERBE) monthly mean clear-sky longwave radiation exitance (LWRE) for April 1985.

The next photograph, also from Harrison et al, 1988, depicts the diurnal range, that is the day-to-night changes, in amount of radiated energy in Wm-2 under cloud-free skies for April 1985. Note that the range of values is much lower than for the previous photograph. Regions having the largest diurnal variation are generally deserts in the subtropical zones. Having few clouds and low humidity (i.e., very little water vapor for greenhouse gas absorption) in the overlying atmosphere, these regions radiate to outer space directly from their surfaces, which range in temperature from over 600C (333K) during the day to near 100C (283 K) at night. You might use these values in the Stefan-Boltzmann equation to calculate the difference in outgoing radiation for these regions and compare your results with the values of about 60 Wm-2 given in the photograph. Note that most ocean regions have very low changes in outgoing radiation (and, therefore, temperature) from day to night.

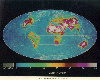Diurnal range of clear-sky LWRE for April 1985.

Now if we consider the effect of clouds, we get a quite different picture. The next photograph (Harrison et al, 1988) shows outgoing radiation, including effects of clouds, averaged over the entire month of April 1985. Comparing this with the clear-sky photograph shown above, you see that the tropical areas have a much lower outgoing longwave radiation. In fact some areas over Indonesia, South America, and Africa on the Equator have temperatures comparable with polar regions. How can this be? A review of the temperature structure of the atmosphere and your observations of cloud patterns from satellite photographs from the third lecture will help answer this question. Very strong surface heating in the tropical regions gives strong convection that creates very deep cloud layers, the tops of which are very high and therefore very cold.

ERBE monthly mean LWRE for April 1985.

The fourth photograph of this set (Harrison et al, 1988) shows the diurnal variation for all days and include the effects of cloudiness. This shows the effect of clouds in reducing the diurnal variation. Note, for instance, that around the margins of the Sahara Desert in Northern Africa the area of high diurnal range shrinks when clouds are present. Clouds tend to keep daytime temperatures lower and nighttime temperatures higher, thereby reducing the diurnal range in two ways.

Diurnal range of LWRE from ERBE for April 1985.

From this you can see that clouds insert a large amount of local variability in the amount of energy the earth radiates to outer space. It also is important to remember that these photographs are averages over many days; if we were to look at a snapshot of a particular day, we would see much more variability from place to place and time to time.

The next map shows a 310-day composite of the outgoing longwave radiation for 10 Januarys (Bess et al, 1989). A notable feature of this plot is that, while the South American and African minima in outgoing longwave radiation are confined to the continental borders, the longitudinally extended minimum in outgoing longwave radiation over Indonesia is much larger and spans a large area of ocean. This particular region of enhanced amount of deep cloudiness will be discussed later when we discuss the Southern Oscillation and El Nino effects.

Contour map of outgoing longwave radiation (OLR) for 10 Januarys.

A similar map (Bess et al, 1989) for a composite of 10 Julys show a general northward seasonal shift, reflecting summer in the Northern Hemisphere and winter in the Southern Hemisphere, and marked reduction of the South American and African cloudiness patterns. The Indonesian pattern has shifted northward and westward to encompass the Indian Monsoon phenomenon. The South American pattern also has evolved into what is known as the Mexican Monsoon. The regions of highest outgoing radiation are again the subtropical high-pressure zones which now have drifted somewhat northward with the movement of the season into North Africa, and the Mediterranean and Middle East Regions.

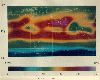Contour map of outgoing longwave radiation (OLR) for 10 Julys.

The final photograph of this set shows the standard deviation of the change in annual outgoing longwave radiation for ten summer (June, July, and August) periods and ten winter (December, January, and February) periods. The standard deviation reveals regions of highest variability from one winter (or summer) season to the next. This shows that June, July and August do not experience large changes from one year to the next but, rather, tend to be reasonably constant. On the other hand, in the Northern Hemisphere winter, a region along the equator has a very high variability: that is, it can be extremely warm one year and quite cool the next. This shows that there is something quite peculiar occurring in this region. We will come back to study this phenomenon in more detail when we consider El Nino.

Standard deviation map of change in interannual OLR for 10 summers (June, July, August) and winters (December, January, February).

One major point that can be concluded from this survey of patterns of outgoing longwave radiation is that clouds play a very significant role in the variability of our weather and climate. Unfortunately clouds are very difficult to describe mathematically in weather and climate models. For this reason, progress in both weather prediction and climate simulation is limited by our ability to characterize the occurrence and effects of clouds. I can't help but be reminded of this in one of my favorite popular songs from several years ago by Judy Collins entitled "Both Sides Now", which has a line that goes 'I've looked at clouds from both sides now, from up and down and still somehow it's clouds illusions I recall, I really don't know clouds at all.'

Excerpt from the song"Both Sides Now by Judy Collins.

Bess, T. Dale, Louis Smith, and Thomas P. Charlock, 1989: A ten-year monthly data set of outgoing longwave radiation from Nimbus-6 and Nimbus-7 satellites. Bull. Amer. Meteor. Soc., 70, 480-489.

Transcription by Theresa M. Nichols