2-2: Climate Models
Eugene S. Takle
© 1997
Understanding climate change is complicated by the many
interactions that occur within the climate system. The next image gives
examples of what are known as "feedback" processes in climate. Feedback
effects occur when a change in one climate parameter changes another,
which, in turn, causes changes in the initial variable. The following are
examples of feedback processes:
1. Temperature-radiation feedback.
The Stefan-Boltzmann equation links temperature and radiated energy
and shows that if the temperature if an object goes up, the energy radiated
also goes up. But this results in a loss of thermal energy from the
object, so its temperature decreases. When an initial increase leads to an
eventual decrease, we call the process a negative feedback.
2. Water-vapor/greenhouse feedback.
Relative humidity is reasonably constant despite variations in
absolute humidity. That is, an increase in temperature leads to more
evaporation and increase in the absolute amount of water vapor in the air.
But since the warmer air has a higher saturation vapor pressure (can hold
more water vapor), the relative humidity stays approximately constant. The
increased absolute humidity, however, increases absorption of infrared
radiation by the atmosphere and hence increases the greenhouse effect.
Note that this increased greenhouse effect raises the surface temperature,
which further increases evaporation. This feedback mechanism is not
self-regulating, so we call it a positive feedback.
3. Snow and ice cover / albedo feedback.
A temperature increase decreases surface area of snow and ice,
which decreases the albedo or reflectivity, which increases the amount of
radiation absorbed and further raises the temperature. This also is a
positive feedback mechanism.
4. Cloudiness / surface-temperature feedback.
As temperature increases, evaporation and relative humidity both
increase leading to more cloudiness. But the increase in clouds reflects
solar energy and also traps more infrared energy from the surface of the
earth. The net effect (which depends on the altitude of the clouds) is
thought to lead to a cooling, which makes this a negative feedback process.
5. Radiative-dynamic coupling.
Increased radiation absorbed at high latitudes due to reduced area
of polar ice will raise temperatures more than at low latitudes, which will
tend to weaken frontal zones and the intensity of frontal storms. This
would lead to complicated changes that might individually be positive or
negative feedback mechanisms.
These feedback processes are described by laws of physics and are
naturally incorporated into climate models. We now focus our attention on
the characteristics of such models.
|
Climate models are essentially the same models that are used every
day for weather forecasting. They have some slight modifications made to
make them adaptable to running for long periods of time (several years as
opposed to a few days), but they use the same basic laws of physics:
conservation of energy, conservation of momentum, conservation of mass, and
an equation of state that describes the relationship of temperature to
pressure and density.
|

Basic equations
of climate
models.
Takle, G.S., 1995 |
The vector equations describing these motions and processes in the
atmosphere are given in the accompanying image. In these equations, the
wind has horizontal components u and v in the east and north directions,
respectively, an vertical component w. T is temperature, p is pressure,
rho is density, g is the acceleration due to gravity, R is the flux of
radiation, omega is the vector describing the angular rotation of the earth
on its axis, F is the frictional force of drag due to the earth's surface,
cv is the specific heat capacity at constant volume, kT is the turbulent
diffusion constant, C represents the effect of heating (or cooling) by
condensation, St includes other unaccounted for sources of heat, q is
specific humidity, S represents sources of water vapor, and Ro is the
universal gas constant. Actual models have three equations rather than
just one for . Separate equations are needed for water vapor, liquid
water, and cloud-ice particles.
|
Some physical process are too complicated or occur at such small
scales that they cannot be resolved by the coarse grid spacing of model and
must be approximated by what are called parameterizations. Cloud
processes, the absorption and radiating properties of the atmosphere and
clouds, and atmospheric interactions with vegetation and other surface
features must be described by parameterizations. The next sketch shows
some of the factors that are taken into account in surface
parameterizations. Vegetation transpires water into the air and suspends
liquid water from precipitation or dew deposition.
The roots, stems, and leaves provide a pathway for subsurface water to be
delivered to the atmosphere. The surface parameterization must account for seasonal change
in vegetation and its change in transpiration, its change in reflective
properties, and its change in drag forces on the atmosphere. Evaporation,
infiltration of water to the deep soil, and surface runoff to streams and
lakes must be taken into account at each time step.
|

Land-surface
parameterization
scheme.
NCAR/TN -
275 +STR
Biosphere-Atmosphere
Transfer Scheme (BATS)
|
For a global climate model we determine values of temperature, wind
speed, pressure, density, and concentration of water vapor, liquid water,
and ice crystals at each of about 50,000 to 150,000 grid points over the
earth at each time step (typically an hour) for the duration of the
simulation (corresponding to the number of pegs in our pinball analogy),
which typically might be a 30-year period (262,800 time steps). As an
estimate of the volume of numbers created by such a model, if 10 variables
are saved for each of 150,000 grid points at 262,800 time steps, the data
to be saved totals 400,000 megabytes.
|
A typical grid used in a global climate model is shown in the next
figure. Each point on this grid has a vertical column of points at which
variables are calculated. The number of points in the vertical direction
ranges from as few as 2 to as many as about 20 levels. Note that typical
global models have a have a horizontal grid spacing of about 500 km ( 300
miles). This means that a single surface grid point must represent all the
surface processes in a box larger than the state of Iowa. Most global
models have resolution too coarse to even recognize the existence of the
Great Lakes, and some completely ignore the Florida peninsula. |
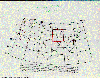
Giss model
|
|
A more desirable grid is given in the accompanying image, but such
fine resolution for a model spanning he entire globe is unmanageably large
with present computational capabilities. Regional climate models, designed
to cover a limited area of the globe as shown in the next image, allow
resolution of more spatial details than global models but require
information from some other source at their lateral boundaries. Using
regional models to study climate change has become a more important
approach in recent years. One such study here at ISU is the
Project to
Intercompare Regional Climate Simulations (PIRCS).
|

High resolution (hypothetical) grid. Cushman and Ferres, Climate Change
Quarterly, 77.
|

Computational domain for a regional climate model. NCAR/TN - 381 +1A. A
user's guide to the Penn State/NCAR mesoscale modelling system.
|
|
We now follow the strategy outlined in the pinball analogy where we
first examine how well the model simulates the characteristics of the
present global climate. The accompanying plot shows the zonally averaged
sea-level pressure. The horizontal axis on this plot gives the latitude
from the North Pole (90o) to the South Pole (-90o). The upper graph gives
the December-January-February (DJF) averages, and the bottom plot gives
June-July-August (JJA) values. Each curve represents a different global
climate model, including the results from the National Center for
Atmospheric Research (NCAR), Geophysical Fluid Dynamics Laboratory
high-resolution model (GFHI), United Kingdom Meteorological Office
high-resolution model (UKHI), NASA Goddard Institute for Space Studies
(GISS), Geophysical Fluid Dynamics Laboratory low-resolution model (GFLO),
United Kingdom Meteorological Office low-resolution model (UKLO), and the
Canadian Climate Centre (CCC). All models use the same basic equations in
simulating climate, but differ in how they parameterize effects of clouds,
radiation, and surface features. The red lines in each of the plots give
the observed zonally averaged sea-level pressure against which results of
all models are to be compared.
|

Zonal-average
mean sea-level
pressure. Adapted from
Figure 4.1 IPCC, 1990.
|
Surface pressure is particularly a good variable to begin the model
comparison because, representing the mass of the atmosphere, it gives the
overall movement of mass over the planet. Notice that the pressure has
maxima about 30o north and south of the Equator. Can you recall the
dominant climatic characteristic of these regions 30o north and south of
the Equator as discussed in an earlier lecture? The minimum near
-70o
marks the pressure minimum of the Southern Hemisphere ocean. Most models
represent the pressure distribution reasonably well except near the polar
regions, especially the South Pole. Recall that the Antarctic continent is
very high with a very deep layer of ice. These factors create severe
difficulties for simulation of pressure over this region. In some cases
(such as UKLO in JJA) a low-resolution model gives results closer to the
observations than high-resolution models. Note that the UKLO model does
not give results as accurate in the DJF simulation.
|
The next plot compares model results for simulating temperature in
for the same two seasons as the previous plot. All models do quite well in
all regions except near the South Pole. Zonal-average precipitation
produced by global models show some of the weakness of climate simulation.
The observations show high-precipitation regions in the tropics (near
latitude 0o) and the mid-latitudes (45o-60oN and S). Most models show the
correct placement of the precipitation maxima, but close examination
reveals that the relative size of the errors typically range from about 20
to 100%. The next plot of this series shows how well models simulate soil
moisture. The models give poor representations of soil moisture in the
Northern Hemisphere. In the tropics where the soil is moist most of the
time, the models do much better. In the subtropical high pressure zones
the soil is usually dry, so again the models do well. So in general, the
models do quite well in areas where the soil moisture doesn't change much
but not very well where there are large fluctuations.
|
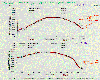 Zonal-average air temperature. Adapted from Figure 4.8 IPCC, 1990.
Zonal-average air temperature. Adapted from Figure 4.8 IPCC, 1990.
|
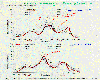 Zonal-average
precipitation. Adapted from Figure 4.10 IPCC, 1990.
Zonal-average
precipitation. Adapted from Figure 4.10 IPCC, 1990.
|
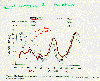 Zonal-average
soil
moisture. Adapted from Figure 4.12 IPCC, 1990. Zonal-average
soil
moisture. Adapted from Figure 4.12 IPCC, 1990.
|
|
The final plot gives results of the latest generation of
high-resolution models. The upper panel shows good agreement except over
Antarctica. The lower panel shows that even the highest resolution for
global models fails to capture such features as the peaks in the tropics
and Southern Hemisphere midlatitudes.
|
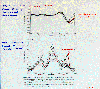
|
Zonally-averaged JJA and DJF
sea-level pressure simulated by current high resolution GCMs.
Adapted from Figure B27 IPCC, 1990.
|
Transcription by Theresa M. Nichols



